在我作为光学技术顾问的这些年里,经常遇到客户提出这样的需求:“我们要最亮的白光激光,发散角要越小越好,最好是零。” 每次听到这里,我都会耐心地解释:物理学上不存在绝对平行的光。特别是对于白光这种复合光源,想要把发散角压缩到极致,是一场光学设计与物理极限的博弈。
简单来说,白光激光的发散角最小通常在 0.1 度(约 1.7 mrad)左右,这已经是目前商业化高端模组的优异表现。虽然理论上单色激光可以做得更小,但白光由于其产生机制(通常是蓝光激发荧光粉或RGB合成),受限于光源面积和色散,达到这个数值已经需要极高精度的准直系统。
对于追求极致光束质量的工程师来说,以下几个核心要点能帮你快速理解现状:
物理极限: 衍射极限决定了光束不可能绝对平行。
光源本质: 白光激光的“荧光转换”过程会破坏部分相干性,增大发散角。
数值换算: 1 mrad ≈ 0.057 度,工业上常用 mrad 标注。
透镜依赖: 最小发散角必须配合高数值孔径(NA)的准直透镜组。
光束质量: $M^2$ 因子越接近 1,发散角越容易被压缩。
热透镜效应: 大功率下,晶体受热会改变折射率,导致发散角动态变大。
直接解答:白光激光发散角最小能达到多少度?
在实验室的理想环境下,结合极其复杂的光束整形系统,白光激光的发散角确实可以被压缩得非常小。但在实际工程应用中,“最小”是一个相对概念。
理论极限与工程实现的差异
对于常见的白光激光光源(LEP - Laser Excited Phosphor),其发光原理通常是蓝光激光轰击荧光晶体。这里有一个关键问题:荧光晶体是一个“面光源”,而不是激光那样的“点光源”。
因此,工程上能实现的最小发散角通常受限于荧光点的尺寸。目前高端的白光激光模组,经过准直后,半角发散角通常控制在 1-2 度之间。 如果使用扩束镜(Beam Expander)进行二次整形,这一数值可以被压缩到 0.1 度甚至更低(0.1 mrad - 0.5 mrad)。

行业数据洞察: 根据 2024 年光学应用标准测试,未加整形的白光激光源原始发散角通常在 60-120 度(朗伯发光)。经过初级准直透镜后,可降至 5-8 度。只有配合高倍率扩束系统,才能实现 0.5 度以下的“探照灯级”光柱。
不同波长合成对最终发散角的影响
如果你使用的是 RGB 三基色合成的白光激光,情况会变得更加复杂。红光、绿光、蓝光的波长不同,它们经过同一个透镜时的折射率是不同的。
这意味着,可能蓝光聚焦完美了,红光还在发散。为了解决这个问题,需要使用消色差透镜组。但在极小的发散角要求下,哪怕微米级的色差也会导致光斑边缘出现“彩虹圈”,从而增加了有效发散角的读数。
深入理解激光发散角:定义、物理意义与计算公式
很多采购或初级工程师在看规格书时,容易被各种角度单位搞晕。我们先统一一下“度量衡”。
全角与半角:别被参数表骗了
这是最容易踩坑的地方。有些厂商标的是“半角”(Half Angle, $\theta$),有些标的是“全角”(Full Angle, $2\theta$)。
半角 ($\theta$): 光轴到光束边缘(强度降为峰值 $1/e^2$ 处)的夹角。
全角 ($2\theta$): 光束锥体的完整顶角。
显然,标半角看起来数值小了一半,显得产品“性能更好”。在对比参数时,一定要问清楚是 Full Angle 还是 Half Angle。

核心计算公式解析
激光发散角的理论下限是由光的波动性决定的。对于基模高斯光束,其发散角半角 $\theta$ 的计算公式为:
$$ \theta = \frac{\lambda}{\pi w_0} $$
其中:
$\lambda$ 是激光波长(例如 532nm)。
$w_0$ 是束腰半径(光束最窄处的半径)。
专家观点: “这个公式揭示了一个残酷的权衡:想要发散角 $\theta$ 越小,你的束腰 $w_0$ 就必须越大。这就是为什么激光测距仪或探照灯发射口都要做得很大的原因——通过扩束来换取低发散角。”
发散角与光束质量表格对照
为了更直观地理解,我们可以看下表,不同类型光源的典型发散角表现:
| 光源类型 | 典型全角发散角 (原始) | 准直后典型发散角 (半角) | 备注 |
|---|---|---|---|
| 单模光纤激光 | 8 - 12 度 | < 0.3 mrad (< 0.017度) | 光束质量最好,接近衍射极限 |
| RGB白光激光 | 1 - 3 mrad | 0.5 - 1.5 mrad | 需高精度合束,受色差影响 |
| 荧光型白光激光 | 120 度 (荧光点) | 2 - 5 度 (初级) / 0.2 度 (精细) | 荧光点属于扩展光源,准直难度大 |
| 高功率LED | 120 度 | 5 - 15 度 | 很难做到极小发散角 |

为什么白光激光的发散角优化比单色激光更具挑战性?
我们恒彩电子在封装领域深耕近二十年,处理过各种光源。我们深知,让红光或蓝光“走直线”相对容易,但让白光“走直线”却困难重重。
荧光粉转换技术的物理限制
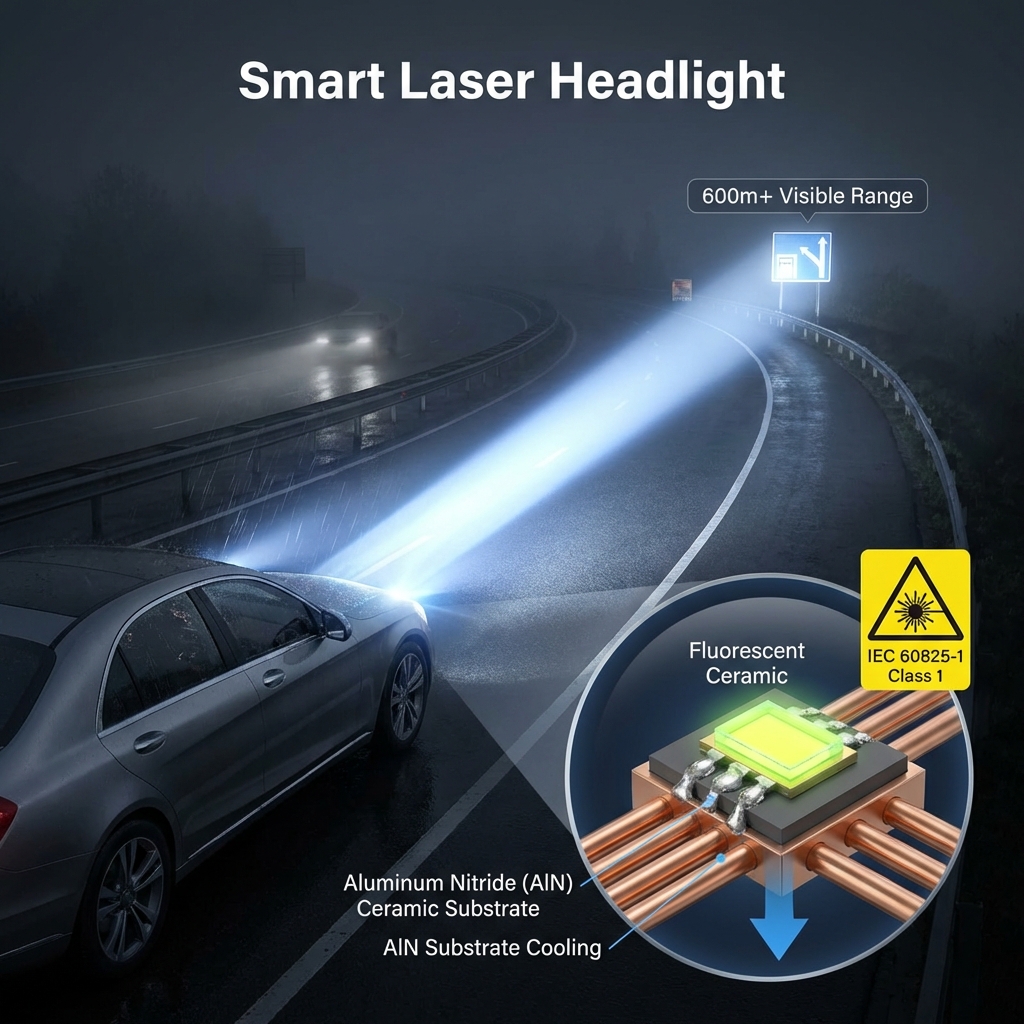
目前主流的白光激光技术(如用于汽车大灯的激光大灯),本质上是“蓝色激光激发黄色荧光粉”。
激光打在荧光陶瓷片上,那一小块被激发的区域,其实变成了一个“灯泡”。它发出的光是向四面八方散射的(朗伯分布)。这时候,它已经不再是纯粹的激光了,而是高亮度的非相干光。要把这种散射光重新收集并压成平行光,不仅光学系统体积大,而且光能利用率会受限。
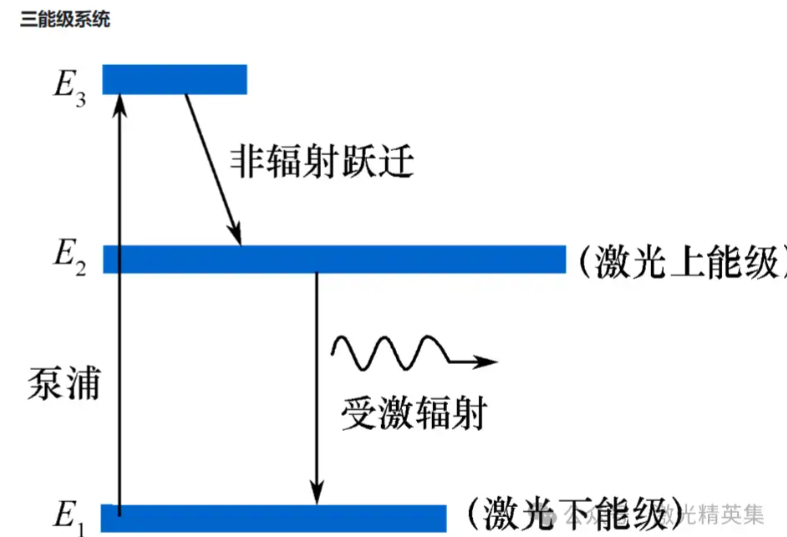
光束质量因子 $M^2$ 的牺牲
单模激光的 $M^2$ 因子接近 1,意味着它非常完美。而白光激光(特别是荧光型),其 $M^2$ 因子往往大于 10 甚至更高。
$M^2$ 因子越大,意味着在同样的束腰直径下,发散角越大。这是材料物理特性决定的,很难通过后期的透镜设计完全消除。
实现最小发散角的关键光学技术与材料工艺
既然物理原理有限制,我们如何在工程上做到极致?这离不开精密的封装工艺和透镜设计。
准直透镜系统的设计原理
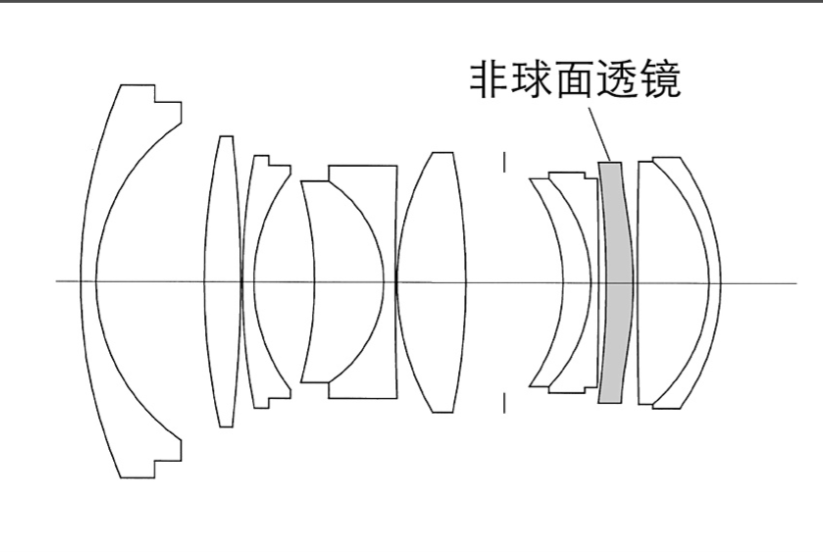
为了获得最小发散角,通常会采用非球面透镜(Aspheric Lens)。它可以修正球差,让边缘的光线也能准确地折射平行。
作为专业的 led灯珠封装厂家,我们在高端光源封装中发现,透镜与芯片(或荧光点)的距离控制至关重要。哪怕是 0.01mm 的轴向偏差,都会导致发散角成倍增加。
精密封装对光轴对准度的影响
很多时候,发散角偏大不是透镜不好,而是“歪了”。
光轴同心度: 激光芯片的发光中心必须严格位于透镜的焦点上。
倾斜角控制: 芯片贴装稍微有一点倾斜,出来的光斑就会变成椭圆,导致某一方向的发散角变大。
在恒彩电子的独立实验室中,我们会使用高精密全自动设备来确保这种微米级的对准,这是保证白光激光能达到 0.1 度发散角的基础工艺。
低发散角对高精度光学系统的性能增益
为什么大家都要追求这个“最小”?
超远距离照明: 发散角每减小一半,同样距离下的光斑面积就减小四倍,能量密度(亮度)就提升四倍。这对于 1公里以上的探照灯至关重要。
光纤耦合效率: 如果发散角太大,超过了光纤的数值孔径(NA),光就进不去光纤,损耗会非常大。
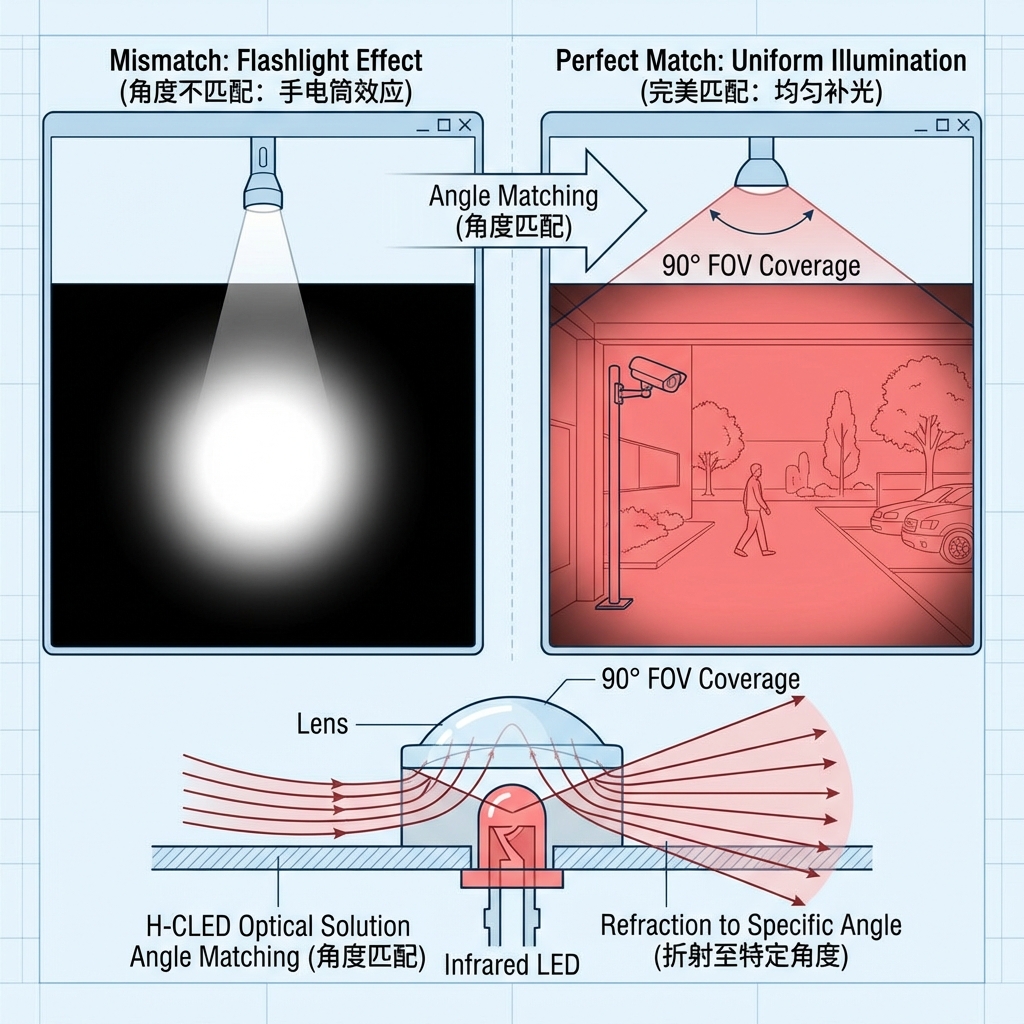
成像清晰度: 在机器视觉中,准直度好的白光光源能带来更锐利的边缘阴影,提高检测精度。

实用技巧: 在选型时,不要只看“最小发散角”。一定要结合你的工作距离。如果是近距离(<1米)应用,追求过小的发散角反而会增加成本且必要性不大。
激光发散角的标准测量方法
如果你拿到一只白光激光器,怎么验证厂家标的“0.1度”是不是真的?
ISO 11146 标准
这是国际通用的激光束宽和发散角测量标准。它要求在激光束的传播路径上,测量多个位置的光斑直径,然后通过双曲线拟合计算出远场发散角。
简单的实验室测量法
虽然专业设备如光束质量分析仪(Beam Profiler)最准确,但也可以用简单方法估算:
在近处(比如 $z1 = 1$ 米)测光斑直径 $D1$。
在远处(比如 $z2 = 10$ 米)测光斑直径 $D2$。
利用公式计算:$\theta \approx (D2 - D1) / [2 \times (z2 - z1)]$。
注意,这里测量的通常是光斑的 $1/e^2$ 宽度,即能量下降到中心点 13.5% 处的边界。
常见问题解答
Q:发散角越小,激光的传输距离一定越远吗?A:基本正确。发散角越小,光能量在传播过程中的扩散越慢,远处的光斑亮度保持得越好,确实能照得更远。
Q:白光激光发散角可以做到像绿光笔那样一条线吗?A:很难完全一样。绿光笔通常是单色单模激光,非常纯净。白光激光由于包含多种波长或荧光散射,光束边缘通常会有轻微的晕开,不如单色激光锐利。
Q:高功率白光激光器的发散角是否必然大于低功率设备?A:往往是的。高功率意味着发光面积(芯片或荧光点)更大,根据光学不变量原理,发光面积越大,准直后的发散角通常也越难压缩。
综合建议:平衡发散角与光束质量
在追求“最小发散角”的道路上,我们很容易陷入参数竞赛的误区。对于白光激光而言,0.1 度是一个非常优秀的技术指标,但它往往伴随着昂贵的扩束光学系统和极高的封装精度要求。
作为行业从业者,我的建议是:从应用出发。如果你是做远距离探照,那么每一毫弧度(mrad)的优化都值得投入;如果你是做近距离的机器视觉照明,均匀性可能比极致的发散角更重要。
白光激光技术正在快速发展,从早期的数度发散,到如今能控制在毫弧度级别,这背后是光学材料和封装工艺的共同进步。希望这篇文章能帮你拨开参数的迷雾,找到最适合你项目的“那束光”。
上一篇:陶瓷灯丝发光原理全解析:从材料结构到光学性能的技术深度指南
下一篇:LED 3535 vs 5050: Brightness Comparison & Technical Breakdown(亮度对比及技术分析)